Net Present Value (NPV)
What is Net Present Value (NPV)?
Net Present Value (NPV) is the value of all future cash flows (positive and negative) over the entire life of an investment discounted to the present. NPV analysis is a form of intrinsic valuation and is used extensively across finance and accounting for determining the value of a business, investment security, capital project, new venture, cost reduction program, and anything that involves cash flow.
NPV Formula
The formula for Net Present Value is:
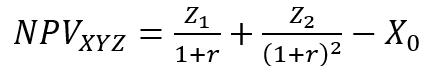
Where:
- Z1 = Cash flow in time 1
- Z2 = Cash flow in time 2
- r = Discount rate
- X0 = Cash outflow in time 0 (i.e. the purchase price / initial investment)
Why is Net Present Value (NPV) Analysis Used?
NPV analysis is used to help determine how much an investment, project, or any series of cash flows is worth. It is an all-encompassing metric, as it takes into account all revenues, expenses, and capital costs associated with an investment in its Free Cash Flow (FCF).
In addition to factoring all revenues and costs, it also takes into account the timing of each cash flow that can result in a large impact on the present value of an investment. For example, it’s better to see cash inflows sooner and cash outflows later, compared to the opposite.
Why Are Cash Flows Discounted?
The cash flows in net present value analysis are discounted for two main reasons, (1) to adjust for the risk of an investment opportunity, and (2) to account for the time value of money (TVM).
The first point (to adjust for risk) is necessary because not all businesses, projects, or investment opportunities have the same level of risk. Put another way, the probability of receiving cash flow from a US Treasury bill is much higher than the probability of receiving cash flow from a young technology startup.
To account for the risk, the discount rate is higher for riskier investments and lower for a safer one. The US treasury example is considered to be the risk-free rate, and all other investments are measured by how much more risk they bear relative to that.
The second point (to account for the time value of money) is required because due to inflation, interest rates, and opportunity costs, money is more valuable the sooner it’s received. For example, receiving $1 million today is much better than the $1 million received five years from now. If the money is received today, it can be invested and earn interest, so it will be worth more than $1 million in five years’ time.
Example of Net Present Value (NPV)
Let’s look at an example of how to calculate the net present value of a series of cash flows. As you can see in the screenshot below, the assumption is that an investment will return $10,000 per year over a period of 10 years, and the discount rate required is 10%.
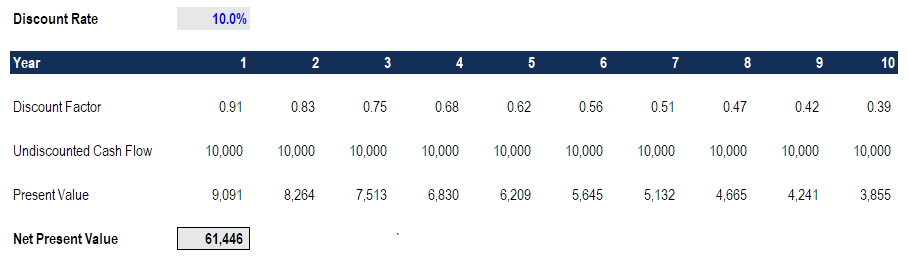
The final result is that the value of this investment is worth $61,446 today. It means a rational investor would be willing to pay up to $61,466 today to receive $10,000 every year over 10 years. By paying this price, the investor would receive an internal rate of return (IRR) of 10%. By paying anything less than $61,000, the investor would earn an internal rate of return that’s greater than 10%.
